2012년04월07일 18번
[과목 구분 없음] 다음과 같은 리벳 이음에서 필요한 최소 리벳 수[개]는? (단, 리벳의 허용전단응력 vsa=200MPa , 허용지압응력 fba=240MPa, 리벳의 직경 d=19mm, 강판의 두께 t=12mm이다)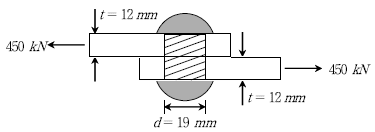

- ① 7
- ② 8
- ③ 9
- ④ 10
(정답률: 54%)
문제 해설
리벳 연결부의 전단응력은 다음과 같이 계산할 수 있다.
τ = F / (π/4 * d^2)
여기서 F는 리벳에 작용하는 전단력이고, d는 리벳의 직경이다.
강판에 작용하는 전단력은 다음과 같다.
F = P * t
여기서 P는 강판에 작용하는 힘이고, t는 강판의 두께이다.
강판에 작용하는 힘은 다음과 같다.
P = N * fba
여기서 N은 필요한 리벳 수이고, fba는 허용지압응력이다.
따라서 리벳 연결부의 전단응력은 다음과 같다.
τ = N * fba / (π/4 * d^2 * t)
이 식에서 τ는 허용전단응력 vsa보다 작아야 한다.
따라서 필요한 리벳 수 N은 다음과 같다.
N = ceil(P / (fba * π/4 * d^2))
여기서 ceil은 올림 함수이다.
이를 계산하면 N은 약 9개이다. 따라서 정답은 "9"이다.
τ = F / (π/4 * d^2)
여기서 F는 리벳에 작용하는 전단력이고, d는 리벳의 직경이다.
강판에 작용하는 전단력은 다음과 같다.
F = P * t
여기서 P는 강판에 작용하는 힘이고, t는 강판의 두께이다.
강판에 작용하는 힘은 다음과 같다.
P = N * fba
여기서 N은 필요한 리벳 수이고, fba는 허용지압응력이다.
따라서 리벳 연결부의 전단응력은 다음과 같다.
τ = N * fba / (π/4 * d^2 * t)
이 식에서 τ는 허용전단응력 vsa보다 작아야 한다.
따라서 필요한 리벳 수 N은 다음과 같다.
N = ceil(P / (fba * π/4 * d^2))
여기서 ceil은 올림 함수이다.
이를 계산하면 N은 약 9개이다. 따라서 정답은 "9"이다.



